walkervova.blogg.se - Advanced sudoku tricks

Advanced sudoku tricks manual#
Advanced sudoku tricks trial#

Advanced sudoku tricks manual#

In manual sudoku solving this technique is referred to as pattern overlay or using templates and is confined to filling in the last values only.Ī library with all the possible patterns may get loaded or created at program start. Ī different approach which also uses backtracking, draws from the fact that in the solution to a standard sudoku the distribution for every individual symbol (value) must be one of only 46656 patterns. One programmer reported that such an algorithm may typically require as few as 15,000 cycles, or as many as 900,000 cycles to solve a Sudoku, each cycle being the change in position of a "pointer" as it moves through the cells of a Sudoku. The disadvantage of this method is that the solving time may be slow compared to algorithms modeled after deductive methods.

The algorithm (and therefore the program code) is simpler than other algorithms, especially compared to strong algorithms that ensure a solution to the most difficult puzzles.

Solving time is mostly unrelated to degree of difficulty.

A solution is guaranteed (as long as the puzzle is valid).

Notice that the algorithm may discard all the previously tested values if it finds the existing set does not fulfil the constraints of the Sudoku. The puzzle's clues (red numbers) remain fixed while the algorithm tests each unsolved cell with a possible solution. The animation shows how a Sudoku is solved with this method. This is repeated until the allowed value in the last (81st) cell is discovered. The value in that cell is then incremented by one. If a cell is discovered where none of the 9 digits is allowed, then the algorithm leaves that cell blank and moves back to the previous cell. When checking for violations, if it is discovered that the "1" is not allowed, the value is advanced to "2". If there are no violations (checking row, column, and box constraints) then the algorithm advances to the next cell and places a "1" in that cell. Briefly, a program would solve a puzzle by placing the digit "1" in the first cell and checking if it is allowed to be there. Although it has been established that approximately 5.96 x 11 26 final grids exist, a brute force algorithm can be a practical method to solve Sudoku puzzles.Ī brute force algorithm visits the empty cells in some order, filling in digits sequentially, or backtracking when the number is found to be not valid. Backtracking is a depth-first search (in contrast to a breadth-first search), because it will completely explore one branch to a possible solution before moving to another branch. Some hobbyists have developed computer programs that will solve Sudoku puzzles using a backtracking algorithm, which is a type of brute force search.

A Sudoku designed to work against the brute force algorithm. Each cell is tested for a valid number, moving "back" when there is a violation, and moving forward again until the puzzle is solved. Mathematical and Computational Algorithms Backtracking A Sudoku (top) being solved by backtracking. Although some niche communities also exist around trying to find the hardest possible puzzles. In general, puzzle makers aim to strike a balance between challenging the player while maintaining the puzzle fun to solve.

Advanced sudoku tricks trial#

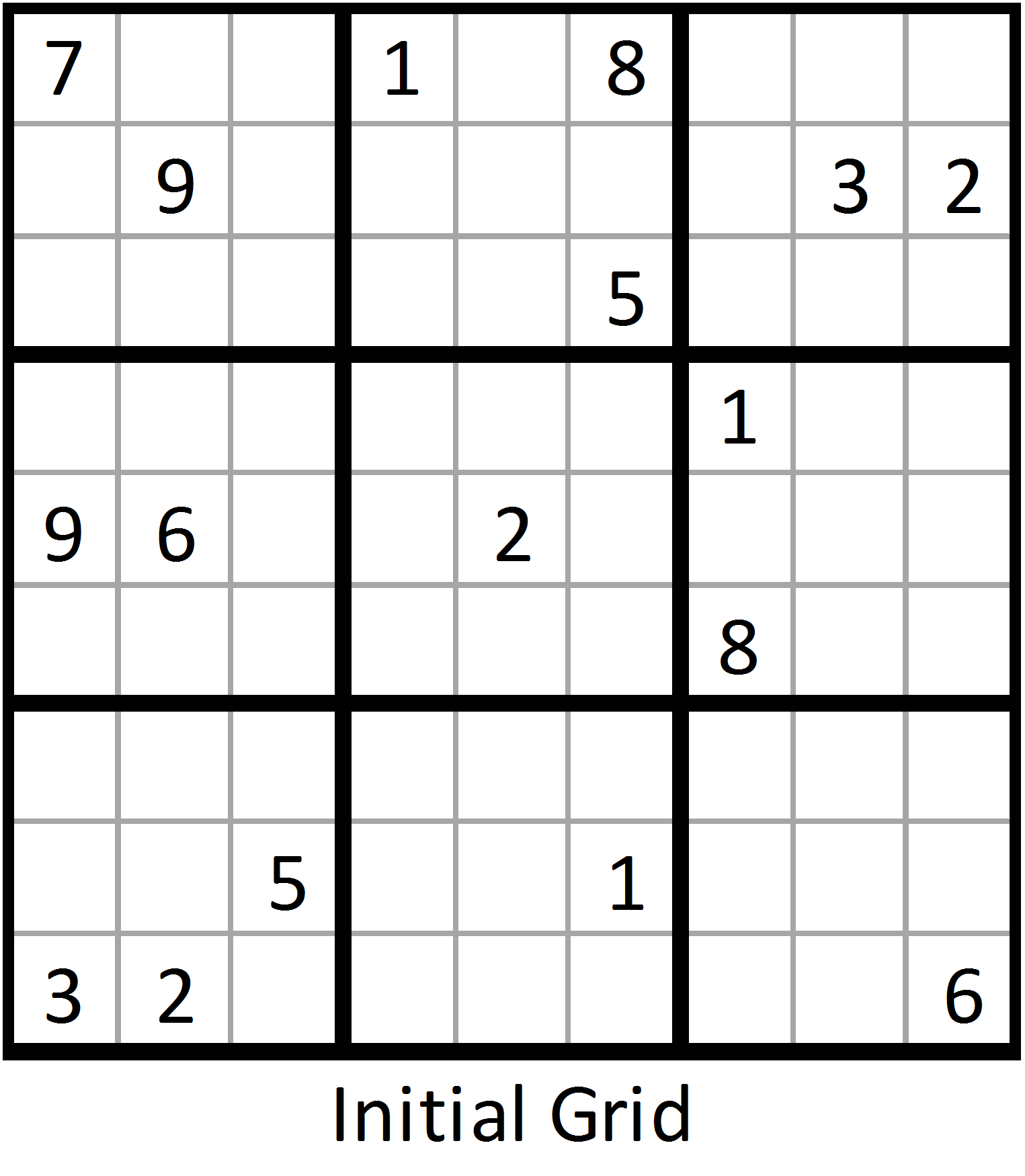
Most published sudoku puzzles of varying difficulties are purposefully constructed to be solvable by a human with pencil and paper techniques, even though it is easier computationally to construct a puzzle without checking if it requires trial and error to solve. There are several computer algorithms that will solve 9×9 puzzles ( n=9) in fractions of a second, but combinatorial explosion occurs as n increases, creating limits to the properties of Sudokus that can be constructed, analyzed, and solved as n increases. Players and investigators use a wide range of techniques to solve Sudokus, study their properties, and make new puzzles, including finding ones with interesting symmetries or other properties. Proper Sudokus have only one unique solution. A Sudoku starts with some cells containing numbers ( clues), and the goal is to solve the remaining cells. Each cell may contain a number from 1 to 9, and each number can only occur once in each row, column, and box. Algorithms to complete a sudoku A typical Sudoku puzzleĪ standard Sudoku puzzle contains 81 cells in a 9×9 grid, further subdivided into 9 separate boxes of 3×3 cells each.